Multi-dimensional arrays and the importance of arrangement

When I wrote about the lockers, I mentioned that the row of lockers was similar to a single dimension array. So, I guess it behooves me[I love to use words like behooves -makes my nose go up in the air, on its own accord ;^)] to talk about some array that has more than a single dimension. As people living in a 3D world, we are all quite comfortable with 2D and 3D but not quite as much with more than 3D [unless we are a theoritical physicists with a penchant for string theory] and hence I believe that understanding 2 dimensional and 3 dimensional arrays should be rather straight forward. But tell you what, in this article, let's not even go to 3D yet [or ever]. Let's make life simpler, and look at a 2D array.

Have you ever been to a small shoe shop? Most of them have at least an entire wall covered with pigeon holes that can hold a single shoe box each. From the floor to the roof, there are rows upon rows of pigeon holes. That entire wall and the bank of shelves there is what a 2D array looks like, and each pigeon hole is an element of that array. Basically, a 2D array is an array of arrays.

In a shoe shop near where I live, works a man, a short man, about 4ft tall on his toes. He is not very educated I think, definitely knows no programming, but nevertheless, can teach us a few things about data structures and algorithms and the importance of good data organization.

As a first step, he has built the 2D array of a shelf (with about 30 columns and 12 rows) on the wall. Then he has arranged the different makes, brands and models of shoes in such a way that each column of pigeon holes contain shoes of one brand and model. So far, so good. So, if we were to go in and ask to see a specific brand and model, he knows which column to go to.

Additionally, he has learnt from experience that the fastest selling shoes are those in sizes 6 through 8, and the next fastest moving sizes being children's sizes 3, 4, and 6. So what he has done is to keep all the shoes of sizes 6, 7, and 8 in pigeon holes that are at a convenient height for him [ in his case, rows 4 through 6]. Children sizes 3, 4, and 6 he has kept in rows 1, 2 and 3 [ for, he finds bending down to reach those shoes easier than having to use the ladder]. All other sizes, the slow moving ones, he has kept in rows 7 to 12. The little diagram below shows a section of the shelf and the arrangement of the shoes.


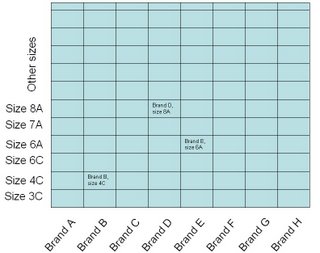
Finally, he has also used some judgement in assigning the various columns to the various brands and models. The more popular ones occupy columns that are closer to where he usually sits, near the entrance of the store, and the less popular ones occupy columns further inside the store.

In this way, he has ensured that he can access the most common brands, models and sizes with the least amount of effort.

Over the next few articles, lets take a leaf out of the shoe seller's book and look at ways of storing and arranging data so as to make our lives easier.

Deleting from Arrays

What do we do when we are done with swimming? We have a shower, take the stuff out of the locker, dress up and leave. Let us skip over the showering part and concentrate on the "take the stuff out of the locker" portion, shall we?
If we breakdown the task further, we can see that what we need to do is:
1. Find our locker
2. Remove the contents of the locker and thereby made the locker empty
3. Leave all other lockers as they were, undisturbed.

How do we find our locker? One way is to have remembered the number/location of our locker. Or the key to the locker had the locker number written on it. That way, we just go straight to the locker [ remember, the lockers are numbered sequentially, so finding the nth locker is a fairly easy step].

If we have not remembered the number of the locker, then we need to open each locker and check if it contains our stuff - a laborious and time-consuming activity.

Removing the contents of the locker is fairly easy - we transfer the contents of our locker into our hand, thereby making the locker empty.

Finally, we leave the other lockers as they are, provided, that is what we want to do. Now, supposing we had used the "fastest draw" method that we had seen earlier in Inserting into arrays part 4 to insert? Then, we may want to move the stuff in other lockers back to where they were before we inserted our stuff. To do that, we will have to repeat our activity of moving the empty locker back to where it was, pretty much the same way we moved it to where we wanted it to be. Try out the code for that yourself, if you can.

Was in IIT on Thursday.

I had a month's dose of fresh, bright faces all in 1 hour! I was in IIT Madras last thursday to address the 4th year Computer science students. It was part of their Industrial Lecture series and I talked about the "essential questions to ask when embarking on a technology startup". Basically, I wanted the students to see the startup in its native environment, namely the business world.

Quite often, as technology people, we tend to look more at the innards of the technological nucleus of the startup and, as they say, miss the woods for the trees, linked lists, arrays and other data structures. This talk was an attempt to see how the startup would need to interact, adjust and live with the outside world entities such as clients, partners, competitors, friends, guides, and VCs, in order to be successful.

The session was fairly interactive and one could see that the students were all a lot more savvy already, than I was until my second startup was spiralling down the drain. I am fairly convinced that the next inflection point in the tech. space will be driven by tech. plays initiated by some of these guys.

I kept the speech short, to about 45 minutes and then had a 15 minute Q&A session and promptly wrapped it up within the stipulated 1 hour - though I wanted to talk on for another hour or so, at least. Anyway, if it was interesting, they will call me again to talk to them and that would give me another chance.

As always, I found the experience of talking to students exhilarating. Thanks Nari, for the opportunity.

Feedback...

Two very nice people who read my blog were a little pessimistic about the chances of people using this blog and benefiting from it.
To quote one, "But really, if someone has the initiative to read the blogs,he/she could probably have read their lessons well".

There is nothing logically wrong with the sentiment. However, the ground reality is that I see a lot of people who seem reasonably smart, have had formal computer science education, and yet don't have a good grasp of the basics of programming. And the few times, I have been forced to recruit such people, I have found that creating an interest in the subject makes them better programmers quite quickly.

So, apart from a possible lack of interest in their chosen area of education, there may be other factors such as uninspired teaching, uninteresting teaching material and excessive emphasis on passing exams involved in creating graduates with no knowledge. Add to this the highly amoral "copy and paste" plagiarism culture juxtaposed with the availability of good material on the ubiquitous net and we have the perfect environment for getting degrees without gaining knowledge!

Anyway, this entry is mainly to convince myself that though there may be some truth in what the two people have said, it may not be the whole truth and so I should gamely continue to write this blog and hope that it is useful for someone somewhere in a way other than as a place to "copy & paste".

What are arrays for?

Before we go into other nice things we can do with arrays, let us look at why we need arrays at all?

Let's say, we have the ages of 6 people and we are asked to write a program to calculate mean(average). What would our program look like?
Maybe something like this:

public double calcAverageAge (int johnAge,
      int janniAge,
      int janardhanAge,
      int AmarAge,
      int AkbarAge,
      int AnthonyAge)
{
   double averageAge = (johnAge + janniAge + janardhanAge + AmarAge + AkbarAge + AnthonyAge)/6;
   return averageAge;
}

Now, supposing, we were to be asked to do the same for 100 or a 1000 people. If we continue with the way we are going, we would soon be up sh*tcreek without a paddle. What we will need is a nice way to access the ages of a 100, 1000 or any reasonable number of people using a single variable.

That is where an array comes in. With an array, our function would look like

public double calcAverageAge (int [] ages, int noOfPeople)
{
   double sumOfAges = 0;
   double averageAge = 0;
   for (int i = 0; i < noOfPeople; i++)
      sumOfAges += ages[i];
   averageAge = sumOfAges/noOfPeople;
   return averageAge;
}
public void callAverage()
{
   int noOfStudents = 100;
   int [] agesOfStudents = new int[100];
/* from file or database fill up the the ages array with values */
   double avgAge = calcAverageAge(agesOfStudents, noOfStudents);
}

As you can see, arrays provide us a nice way to handle situations where we have to access and manipulate many variables of the same data type.

Every once in a while, we should take our heads out of the details and look for the "raison d'etre", question the obvious, take a closer look at the trees, whatever.

Inserting into arrays – part 4

In the article First look at arrays we saw one more way of inserting our stuff into the locker which was nice and easy.
Quote(from the earlier article):
"In another way of going about it, you would probably start at the locker before the empty one (locker n-1) and transfer all the items in that into the empty one. Then you would move to the previous locker (locker n-2) and move the items in that into the currently empty one (locker n-1). You will keep doing this (quickly – before anybody comes in) until the locker you are interested in is empty. Then you can put your things in – mission accomplished and most probably no one will notice that their stuff has been shifted by one locker! The second approach required only one hand and had the added benefit of being able to look nonchalant and guilt free if anyone walked in while you were half way through the exercise!"

Let us look at the code for that:
Already we have the findEmptyLocker function written. We shall write that function again (with a minor change) so that we don’t have to scroll all the way down to the first article to see it.

public int findEmptyLocker(int insertPos)
    {
    for (int i=insertPos; i < 10; i++)
    {
         if (arr[i].content.equalsIgnoreCase("empty"))
              return i;
     }
    return -1;
}

Now we can write the new function which we will call insertIntelligently. It looks like

public void insertIntelligently(int insertPos, String myStuff)
{
    int pos = findEmptyLocker(insertPos);
    if (pos != -1)
    {
         for (int i = pos; i > insertPos; i--)
              arr[i].content = arr[i-1].content;
         arr[insertPos].content = myStuff;
    }
}

First we find the first empty locker at or to the right of the locker we are interested in.
Once we find it, we move the contents of the locker just before the empty one into the empty one. What we have effectively done is moved the empty locker closer by one slot to where we want it to be! This is the magic I was talking about. We keep doing this until the empty locker is where we want it to be. Having done that, we come out of the for loop and then insert our stuff into the empty locker. Done.
The logic is elegant. We have not used any temporary storage/variables. The code is efficient. What more can we ask for?

The articles on arrays that we have seen so far illustrate a few basic concepts. One is that there are many ways of doing the same thing. Some ways will be better than others, so we should think of at least a few different ways of achieving our goals before comparing them and arriving at the best way forward.
Second, if we can find a real-life analogy to our algorithm, we are able to better grasp the logic behind it.
One caveat: The way we do things physically/mentally need not necessarily be the best way for the computer. Gradually we will have to learn to think in more abstract terms so that we can exploit the inherent strengths of the computer.

Arrays, indexes and memory

Before we go into the next article on inserting into arrays, I thought we could take a quick detour to answer one of the questions we had raised earlier:
Why do array indexes go from 0 to n-1 in languages like java, C, C++, etc?

In order to understand the reasons, we need to understand how memory is allocated for variables in general and arrays in particular.

Let us imagine the computer memory to be a large tract of land owned by the government. Whenever we want some land, we can approach the government and they will provide us the land we want, if available, as long as it is for a fixed time period, we agree to use it only to build temporary structures and we promise to return it back to the government when we are done using it.

When the government allocates the land to us, they ensure that no piece of it has already been allocated to anybody else. They also assume that we will not usurp/use any land outside of what has been allocated to us.

Some governments will keep a close watch to ensure that we do not build outside our area, while other more liberal governments will leave that responsibility with us.

If we have asked for place for 10 stalls and surreptitiously or unknowingly build the 11th one, we could end up building our stall on top of somebody else’s toilet, for example. Then when they use their toilet (or what used to be their toilet), they may end up pooping on our sofa creating a mess all around. This is exactly what happens when we misuse memory and overwrite some other variable – in unix the system will crash with a “core dump” message – kind of apt for our analogy, don’t you think?

We could ask for, say,
(1) 1000 sq. meters of land in order to put up my circus tent for a period of one month, or
(2) some contiguous space for a dozen 10 meters wide (and 20 meters long) stalls for me to run a carnival for the next one week.

The first request above is similar to asking for space for a primitive data type or a structure:

Int i;
Exchanger e = new Exchanger();

The second request is similar to asking for an array, and each stall is an element in that array, each element being the same size.

int [] intArray = new int[12];

The government will probably tell you that your area starts at a particular point and extends till some other point. The lease agreement will be for the period you have requested the land for (the scope of the variable).

Our location provided by the government is the starting address of our piece of land, which incidentally, in the second case, is also the starting address of our first stall.

Leaving the land analogy behind, we can now see how this maps to arrays.
The array variable contains the starting address of the entire memory that has been given to us, which incidentally, is also the starting address of the first element.
So the address of each of the elements can be calculated as
Address of first element = starting address of array + 0 * size of each element.
Address of second element = starting address of array + 1 * size of each element
Address of nth element = starting address of array + (n-1) * size of each element.

So it is only natural, in the programming world, that we give the array subscripts ranging from 0 to n-1. This is quite counter-intuitive for us [who has heard a door number 0, for example?] and thus some languages, like most variations of BASIC, have chosen to go with subscripts ranging from 1 to n. They would internally calculate the address of the different elements as
Address of first element = starting address of array + (1-1)* size of each element.
Address of second element = starting address of array + (2-1) * size of each element.
Address of nth element = starting address of array + (n-1) * size of each element.
Which as you can see is identical to the previous set of formulae.
I hope this has given you a brief idea about memory allocation and management.
Next article will be about the 3rd insertion technique I promised to write.